 Navegación
Navegación Sara de la Rosa de Sáa. Doctora en Matemáticas y Estadística
Oficina de Evaluación de Tecnologías Sanitarias del Principado de Asturias (OETSPA)
Supongamos que un médico recibe a un paciente del que se sospecha que tiene una determinada enfermedad. La medicina está gobernada por la incertidumbre, por lo que los pasos que dé el médico hasta emitir un diagnóstico los hará en el marco de la probabilidad.
Puede que en vista de los síntomas y anamnesis hecha al paciente, el médico deseche el realizar una prueba diagnóstica, bien porque considere muy baja la probabilidad de tener la enfermedad o bien porque, al contrario, sea un caso claro que puede ser diagnosticado sin tener que recurrir a más pruebas. Si el médico tiene una duda razonable decidirá realizar alguna prueba diagnóstica cuyo objetivo será reducir el nivel de incertidumbre lo suficiente como para tomar una decisión con respecto a la existencia o no de la enfermedad.
Antes de realizar una prueba, se asigna al paciente una probabilidad pretest de tener la enfermedad (se suele tomar la prevalencia). Después de la prueba, según los resultados de la misma, le asignaremos una nueva probabilidad llamada probabilidad postest. La utilidad de la prueba realizada viene determinada por la reducción del grado de incertidumbre que produzca, bien sea en el sentido de confirmar la enfermedad o bien en el de descartarla.
Sensibilidad y especificidad
Las pruebas diagnósticas no son perfectas. Si un paciente tiene la enfermedad y realizamos como prueba un determinado test, es lógico esperar un resultado positivo (Verdadero Positivo, VP), pero puede salir negativo (Falso Negativo, FN). Si, al contrario, el paciente no tiene la enfermedad (sano), lo lógico sería esperar un resultado negativo (Verdadero Negativo, VN), pero puede salir positivo (Falso Positivo, FP).
Consideremos los N individuos de nuestra población (o los de la muestra si es el caso) objeto de estudio que clasificaremos en enfermos y sanos mediante la prueba de referencia gold standard. A cada individuo lo someteremos a una prueba o test (T) que podrá resultar positivo (T+) o negativo (T-). Podemos resumir la información recogida en una tabla de contingencia o de doble entrada:
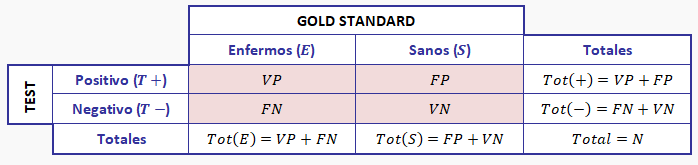
Tabla 1. Modelo de tabla de contingencia que muestra la relación entre el resultado de un test diagnóstico y la presencia o ausencia de una enfermedad
Una característica importante de la calidad de un test es la validez o capacidad para medir adecuadamente lo que se pretende estudiar. En una primera aproximación se puede tomar como validez la proporción de pacientes correctamente diagnosticados por el test. Estos pacientes serían los VP y los VN y, por tanto,
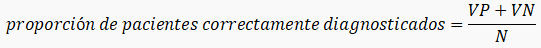
Pero más importante que esta proporción global de aciertos son las proporciones de aciertos dentro de los subgrupos de los enfermos y de los sanos. Surgen así dos indicadores:
- Sensibilidad (Sen): es la probabilidad de que el test resulte positivo sabiendo que el paciente está enfermo:
- Especificidad (Esp): es la probabilidad de que el test resulte negativo sabiendo que el paciente está sano:
Ejemplo 1: supongamos que la sensibilidad de un test es igual a 1=100%.
a) Si un test resulta positivo, ¿se puede asegurar que el paciente está enfermo?
b) Si un test resulta negativo, ¿se puede asegurar que el paciente está sano?
Solución:
Si la sensibilidad es igual a 1=100%, se debe cumplir que
igualdad que solo es cierta si VP=VP+FN, es decir, FN=0, lo que se refleja en la tabla:

Tabla 2. Relación entre el resultado del test diagnóstico y la presencia o ausencia de la enfermedad cuando la sensibilidad del test es igual a 1=100%
Podemos ahora responder más fácilmente a los dos apartados.
a) No, pues según vemos en la tabla puede ser un falso positivo (FP) de una persona sana. Pensar, por ejemplo, en un test que por error de fabricación diese siempre positivo. La sensibilidad sería 1, pero todos los sanos habrían dado también positivo.
b) Sí, pues según vemos en la tabla no hay ningún falso negativo (FN=0), por lo que el negativo del test debe corresponder sin duda a una persona sana (VN).
El ejemplo anterior nos lleva a decir que “si la sensibilidad es alta (mayor o igual que 0.95=95%) y el test resulta negativo, habrá fuertes razones para afirmar que el paciente es sano”. Nada puede decirse si el resultado del test es positivo.
Ejemplo 2: supongamos que la especificidad de un test es igual a 1=100%.
a) Si un test resulta positivo, ¿se puede asegurar que el paciente está enfermo?
b) Si un test resulta negativo, ¿se puede asegurar que el paciente está sano?
Solución:
Si la especificidad es igual a 1=100%, se debe cumplir que
igualdad que solo es cierta si VN=FP+VN, es decir, FP=0, lo que se refleja en la tabla:
Tabla 3. Relación entre el resultado del test diagnóstico y la presencia o ausencia de la enfermedad cuando la especificidad del test es igual a 1=100%
Podemos ahora responder más fácilmente a los dos apartados.
a) Sí, pues según vemos en la tabla no hay ningún falso positivo (FP=0), por lo que el positivo del test debe corresponder, sin duda, a una persona enferma (VP).
b) No, pues según vemos en la tabla puede ser un falso negativo (FN) de una persona enferma. Pensar, por ejemplo, en un test que por error de fabricación diese siempre negativo. La especificidad sería 1, pero todos los enfermos habrían dado también negativo.
El ejemplo anterior nos lleva a decir que “si la especificidad es alta (mayor o igual que 0.95=95%) y el test resulta positivo, habrá fuertes razones para afirmar que el paciente es enfermo”. Nada puede decirse si el resultado del test es negativo.

Según se desprende de los dos ejemplos anteriores, lo ideal sería tener un test en el que tanto la sensibilidad como la especificidad fuesen 1=100%, pero esto no va a ser posible. Si tenemos que elegir, ¿en qué situaciones es mejor elegir una prueba de alta sensibilidad y en cuáles una de alta especificidad? Sabiendo que una alta sensibilidad reduce el número de FN y una alta especificidad reduce el número de FP, la pregunta anterior la transformamos en esta otra: ¿en qué situaciones es mejor reducir el número de FN y en cuáles el de FP?
Si tratamos de confirmar una enfermedad, hay que usar pruebas de alta especificidad para reducir el número de FP, de forma que si la prueba nos da positiva haya gran probabilidad de que sea un VP.
Por el contrario, si estamos tratando de confirmar la ausencia de enfermedad deberemos optar por una prueba de alta sensibilidad que reduzca el número de FN, de manera que si el resultado de la prueba es negativo haya gran probabilidad de que se trate de un VN.

Por último, indicar que tanto la sensibilidad como la especificidad son valores intrínsecos a cada prueba. No dependen de la prevalencia de la enfermedad, pues en sus definiciones no interviene para nada el total de individuos de la población. Son, en definitiva, valores fijos para cada prueba y se pueden aplicar a cualquier población.
Valores predictivos
La sensibilidad y la especificidad nos sirven para medir la validez de una prueba o test diagnóstico pero conociendo de antemano si el paciente es enfermo o sano.
Pero desde un punto de vista clínico, lo importante es trabajar con pacientes aún sin clasificar y calcular la probabilidad de estar enfermo o sano según la prueba o test diagnóstico resulte positivo o negativo respectivamente, es decir, P(Enfermo/T+) y P(Sano/T-).
Supongamos una población de N individuos con prevalencia conocida para una determinada enfermedad. Un médico recibe a uno de ellos y tras la anamnesis y exploración iniciales tiene dudas razonables sobre la presencia o ausencia de dicha enfermedad, por lo que decide realizar una prueba diagnóstica de sensibilidad y especificidad también conocidas. Definimos:
- Valor predictivo positivo (VPP): es la probabilidad de que el paciente esté enfermo si el test ha resultado positivo:
La interpretación del VPP es clara: se trata de la probabilidad postest de tener la enfermedad si el resultado del mismo ha sido positivo.
- Valor predictivo negativo (VPN): es la probabilidad de que el paciente esté sano si el test ha resultado negativo:
La interpretación del VPN es igualmente clara: se trata de la probabilidad postest de no tener la enfermedad si el resultado del mismo ha sido negativo.
El valor predictivo positivo hemos dicho que es la probabilidad postest de tener la enfermedad si el resultado de la prueba es positivo, pero, ¿cuál es la probabilidad postest de tener la enfermedad si el resultado de la prueba es negativo? Aplicando una de las propiedades de la probabilidad:
Análogamente, la probabilidad de estar sano si el resultado de la prueba es positivo sería:
Ejemplo 3: si en una población de 1000 individuos la prevalencia de una determinada enfermedad es 0.1 y el test diagnóstico que se aplica tiene una sensibilidad igual a 0.8=80% y una especificidad igual a 0.9=90%, hallar los valores predictivos.
Solución:
Con los datos del enunciado, construimos la siguiente tabla de doble entrada:
Tabla 4. Relación entre el resultado del test diagnóstico y la presencia o ausencia de la enfermedad correspondiente al Ejemplo 3
Por lo que:
El alto valor del VPN nos indica que hay gran probabilidad (97.59%) de que un paciente no esté enfermo cuando el test resulte negativo. No sirve en cambio de mucho el VPP, pues su valor es bajo.
Como ya dijimos, la sensibilidad y la especificidad no dependen de la prevalencia de la enfermedad, siendo sus valores los mismos aunque se apliquen a poblaciones de distinta prevalencia. Sin embargo, no ocurre lo mismo con los valores predictivos que sí dependen de la prevalencia, variando sus valores cuando esta cambia.

Ejemplo 4: consideremos el mismo enunciado del ejemplo anterior cambiando solo el valor de la prevalencia a 0.9.
Solución:
La tabla quedaría ahora como sigue:
Tabla 5. Relación entre el resultado del test diagnóstico y la presencia o ausencia de la enfermedad correspondiente al Ejemplo 4
Y en cuanto a los valores predictivos:
El alto valor del VPP nos indica que hay gran probabilidad (98.63%) de que un paciente esté enfermo cuando el test resulte positivo. No sirve en cambio de mucho el VPN, pues su valor es bajo.
Según pudimos ver en los dos ejemplos anteriores, cuando la prevalencia es baja, el VPP será bajo y el VPN alto. Al contrario, si la prevalencia es alta, el VPP será alto y el VPN bajo.
La relación entre la prevalencia y los valores predictivos podemos verla resumida en la tabla siguiente.
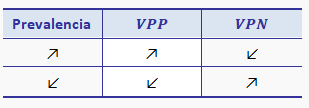
Tabla 6. Relación entre prevalencia y valores predictivos
Razones de verosimilitud
Hemos visto que los valores predictivos permiten hallar la probabilidad postest de tener la enfermedad, tanto si el resultado del test es positivo como si es negativo. Sin embargo, como dependen de la prevalencia, sus valores cambian, y el valor obtenido para una determinada población varía al obtenerlo en otra población de prevalencia distinta.
Sería conveniente, por tanto, otro enfoque que nos ayude a tomar decisiones utilizando solo la sensibilidad y la especificidad (que son valores conocidos y fijos para un test), prescindiendo de la prevalencia. Para ello, vamos a introducir las llamadas razones de verosimilitud (RV), conocidas también con el nombre de cocientes de probabilidades o likelihood ratios.
Estas razones de verosimilitud comparan la probabilidad de obtener un determinado resultado (positivo o negativo) en la prueba o test diagnóstico en pacientes enfermos, con la probabilidad de obtener el mismo resultado en pacientes sanos. Concretamente, definimos:
- Razón de verosimilitud positiva (RV+): es la probabilidad de obtener un resultado positivo en el test en un paciente enfermo dividida por la probabilidad de obtener el resultado positivo en un paciente sano:
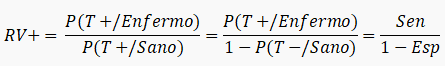
- Razón de verosimilitud negativa (RV-): es la probabilidad de obtener un resultado negativo en el test en un paciente enfermo dividida por la probabilidad de obtener el resultado negativo en un paciente sano:
¿Cómo interpretar estas razones? El resultado de una división nos dice cuántas veces mayor es el numerador que el denominador. Por tanto, la razón de verosimilitud positiva se interpreta como cuántas veces es más probable obtener un resultado positivo en el test en un paciente enfermo que en un sano. Análogamente, la razón de verosimilitud negativa se interpreta como cuántas veces es más probable obtener un resultado negativo en el test en un paciente enfermo que en un sano.
Según los valores de las razones de verosimilitud, la calidad de la prueba o test diagnóstico suele evaluarse utilizando las siguientes tablas.
Tablas 7 y 8. Relación entre la RV+ y la calidad del test (izquierda) y la RV- y la calidad del test (derecha)
De la interpretación de las razones de verosimilitud vemos que nos interesa que la RV+ sea mayor que 1 y lo mayor posible, y la RV- menor que 1 y lo más pequeña posible. Observemos que los valores utilizados para la RV- en la Tabla 8 son menores que 1, por lo que si para una más clara interpretación usamos sus inversos, obtenemos los mismos valores utilizados para la RV+ en la Tabla 7 (de ahí que las otras dos columnas sean idénticas en ambas tablas).
Ejemplo 5: realizamos un test de antígenos para el COVID-19 con sensibilidad=96.52% y especificidad=99.68%. Hallar las razones de verosimilitud e interpretarlas. El resultado del test ha sido negativo.
Solución:
Este resultado nos dice que es más de 300 veces más probable que el test resulte positivo en un enfermo que en un sano.
Este resultado nos dice que es 0.0349 veces más probable que el test resulte negativo en un enfermo que en un sano. Dado que esto no resulta muy claro, es mejor dar la interpretación mediante el inverso del resultado (1/0.0349=28.69) y decir que es unas 30 veces más probable que el test resulte negativo en un sano que en un enfermo.
Se trata de un test muy fiable y el resultado negativo nos dice que tenemos probabilidad muy alta de no tener la enfermedad.
Una de las principales aplicaciones de las razones de verosimilitud es que permiten pasar de la probabilidad pretest de tener la enfermedad a la probabilidad postest de tenerla. También podremos hallar los valores predictivos a partir de ellas sin necesidad de construir la tabla de contingencia o aplicar el teorema de Bayes. No obstante, sí tendremos que dar la prevalencia, pues sabemos que estos valores dependen de ella.
En conclusión, la interpretación de los resultados de las pruebas diagnósticas requiere un enfoque probabilístico, en el que la sensibilidad, especificidad, valores predictivos y razones de verosimilitud juegan un papel fundamental. Cada indicador aporta información distinta sobre la calidad del test y comprender su significado permite tomar decisiones más precisas, confirmando o descartando enfermedades de manera más segura y fundamentada.
Destacados
- Volumen y resultados: ¿es hora de un paso adelante en la regionalización de la cirugía?
- Prescripción potencialmente inadecuada en dos centros socio-sanitarios según los criterios START-STOPP
- Guía Farmacoterapéutica (GFT) unificada para hospitales del Servicio de Salud del Principado de Asturias
- Biblioteca del Hospital Universitario Central de Asturias
- Sistema de vigilancia del cáncer laboral en el Principado de Asturias Nota 1: Programa de detección y comunicación de cáncer profesional
Sugeridos desde E-Notas
- Nueva Biblioteca Virtual gcSalud: un recurso clave para el Sistema Sanitario Público del Principado de Asturias
- ¿Podrá la inteligencia artificial mejorar la productividad del sistema sanitario?
- Conceptos probabilísticos en la toma de decisiones en salud. (II) Evaluación de las pruebas diagnósticas
- La incertidumbre y el análisis de bienestar de las prestaciones médicas o el nacimiento de la economía de la salud
- Guía Terapéutica Antimicrobiana del Sistema Nacional de Salud: Abordaje de los procesos de la cavidad bucal